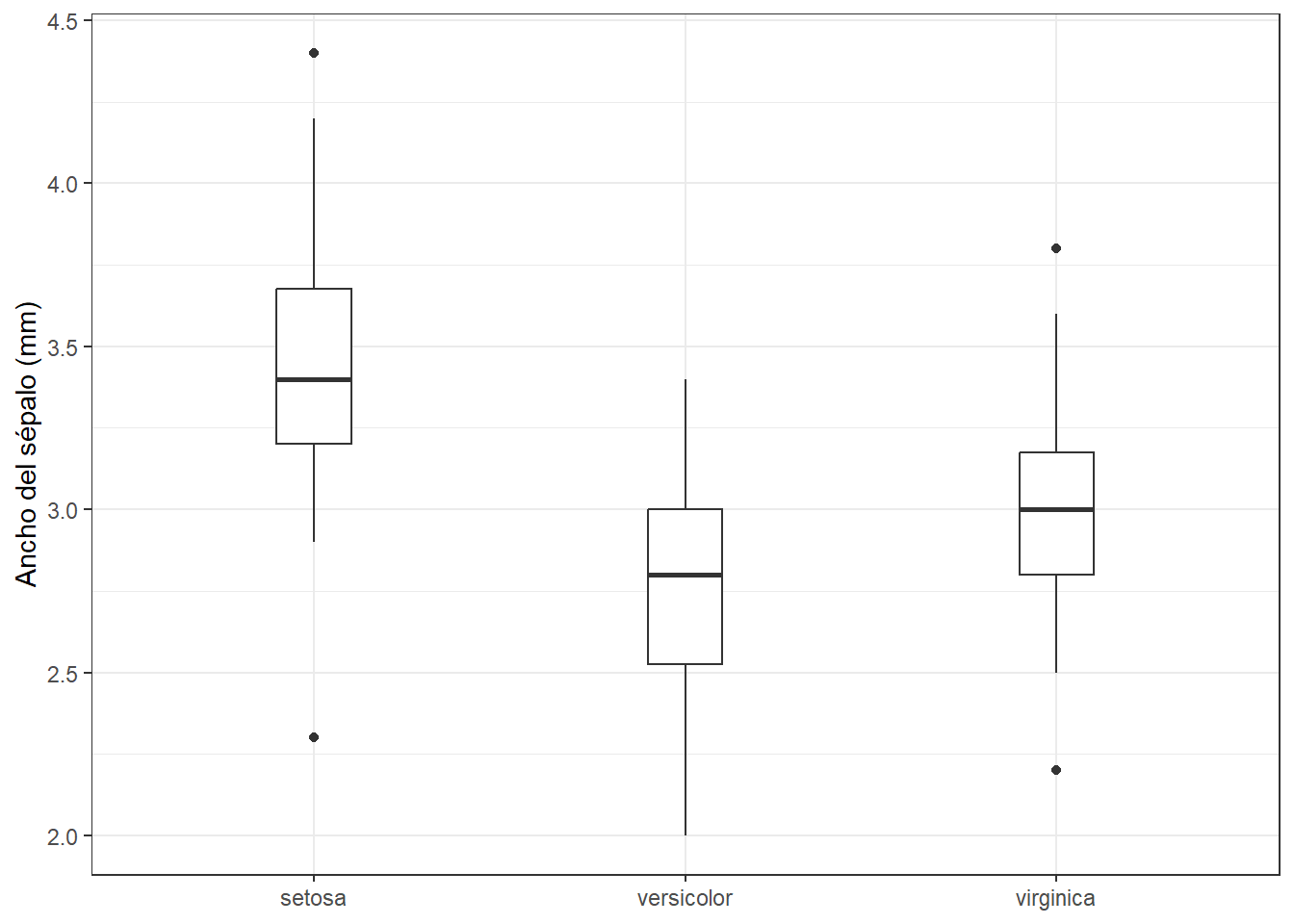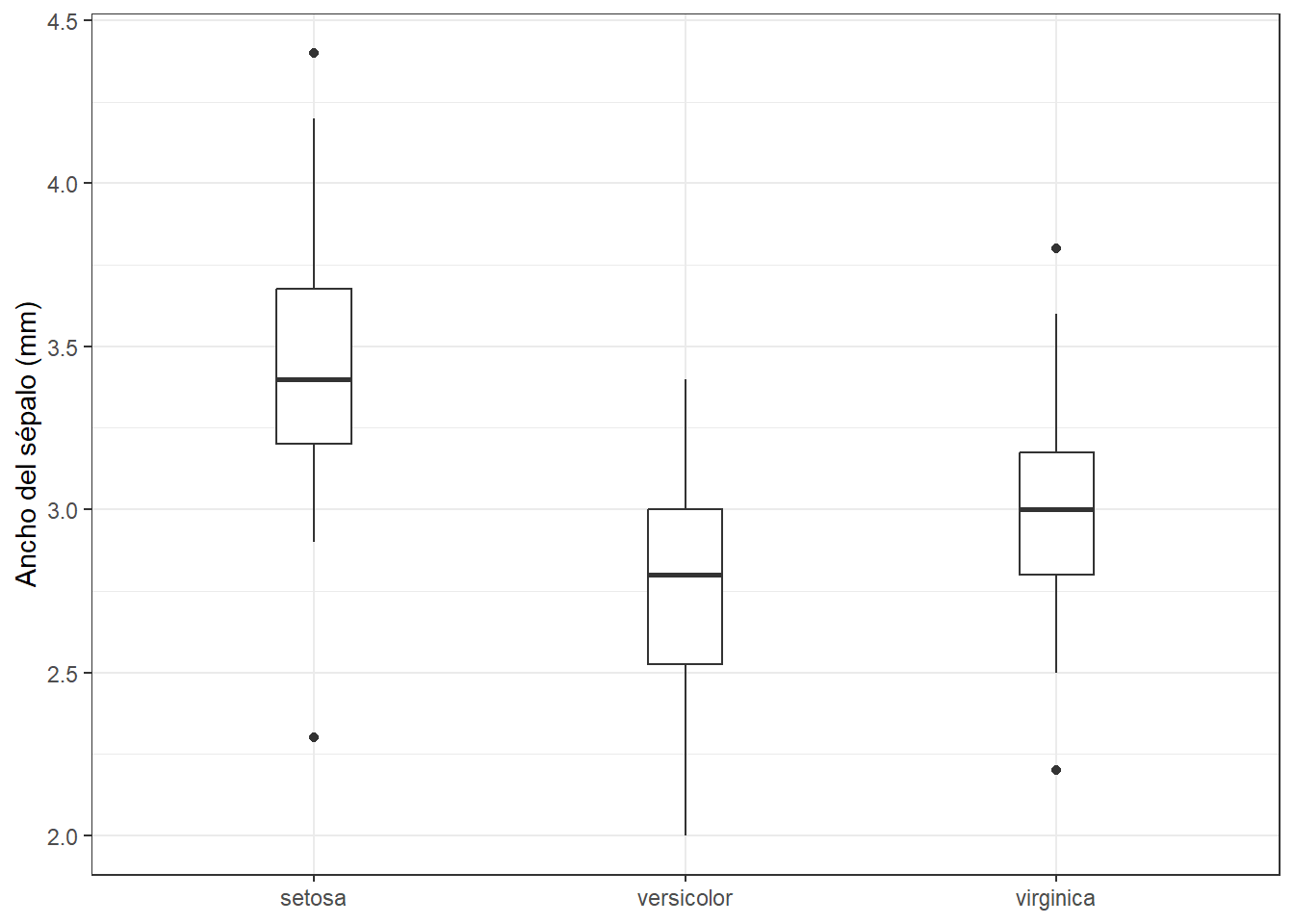8 Sistemas de Coordenadas

Los sistemas de coordenadas se encargan de combinar las estéticas de posición (x, y) para crear un gráfico en dos dimensiones. Estas controlan aspectos como:

La escala de los ejes.
La proyección de los datos.
La orientación de los ejes.

En general, se pueden dividir los sistemas de coordenadas en dos grupos (Wickham, Navarro, y Pedersen 2021):

Lineares: mantienen la forma de las geometrías.
No lineares: modifican la forma de las geometrías.

En este capítulo vamos a trabajar con dos datasets:

iris: dataset donde se han medido la longitud y anchura de pétalos y sépalos de 150 flores, además de la especie a la que pertenecen (ver Tipos de visualización).
inventario: dataset con datos de inventario de 27 parcelas en los que se ha medido el DBH, altura y especie (ver Sección 2.2).

Para comenzar, vamos a cargar los paquetes necesarios y a leer los datos que utilizaremos en este capítulo.

library(tidyverse)
library(patchwork)

8.1 Sistemas lineares

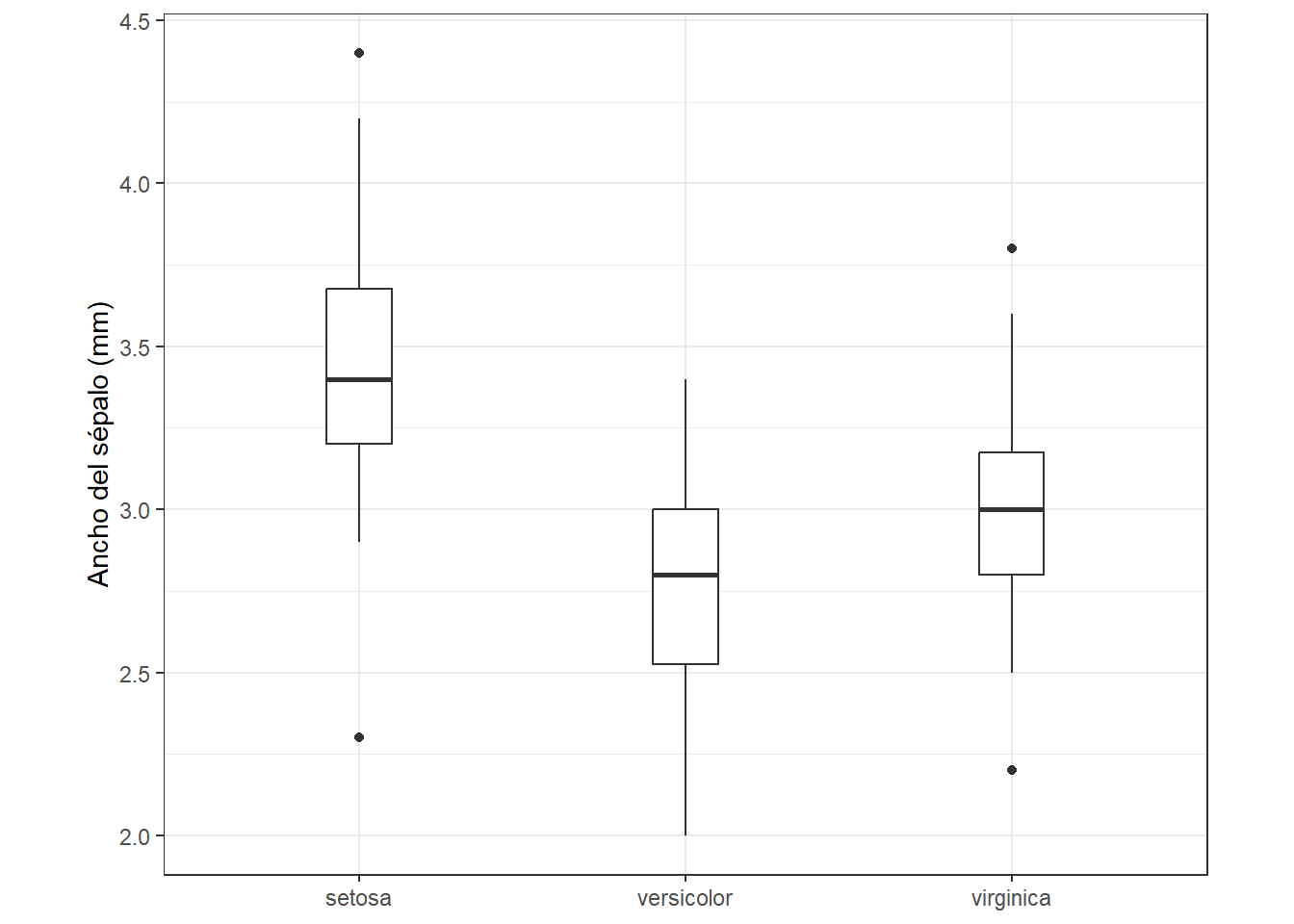
Tenemos tres funciones principales para trabajar con sistemas de coordenadas lineales. Una de estas, es la que viene por defecto en ggplot2 que es coord_cartesian(). Vamos a partir del siguiente gráfico:

boxplot_base <- iris |> 
    ggplot(aes(x = Species, y = Sepal.Width)) +
    geom_boxplot(
        width = .2
    ) +
    theme_bw() +
    labs(
        x = NULL,
        y = "Ancho del sépalo (mm)"
    )

boxplot_base

Fig. 8.1: Distribución del ancho del sépalo

En el siguiente tabset, vamos a ver la función coord_cartesian() y cómo se puede utilizar para modificar los límites de los ejes.

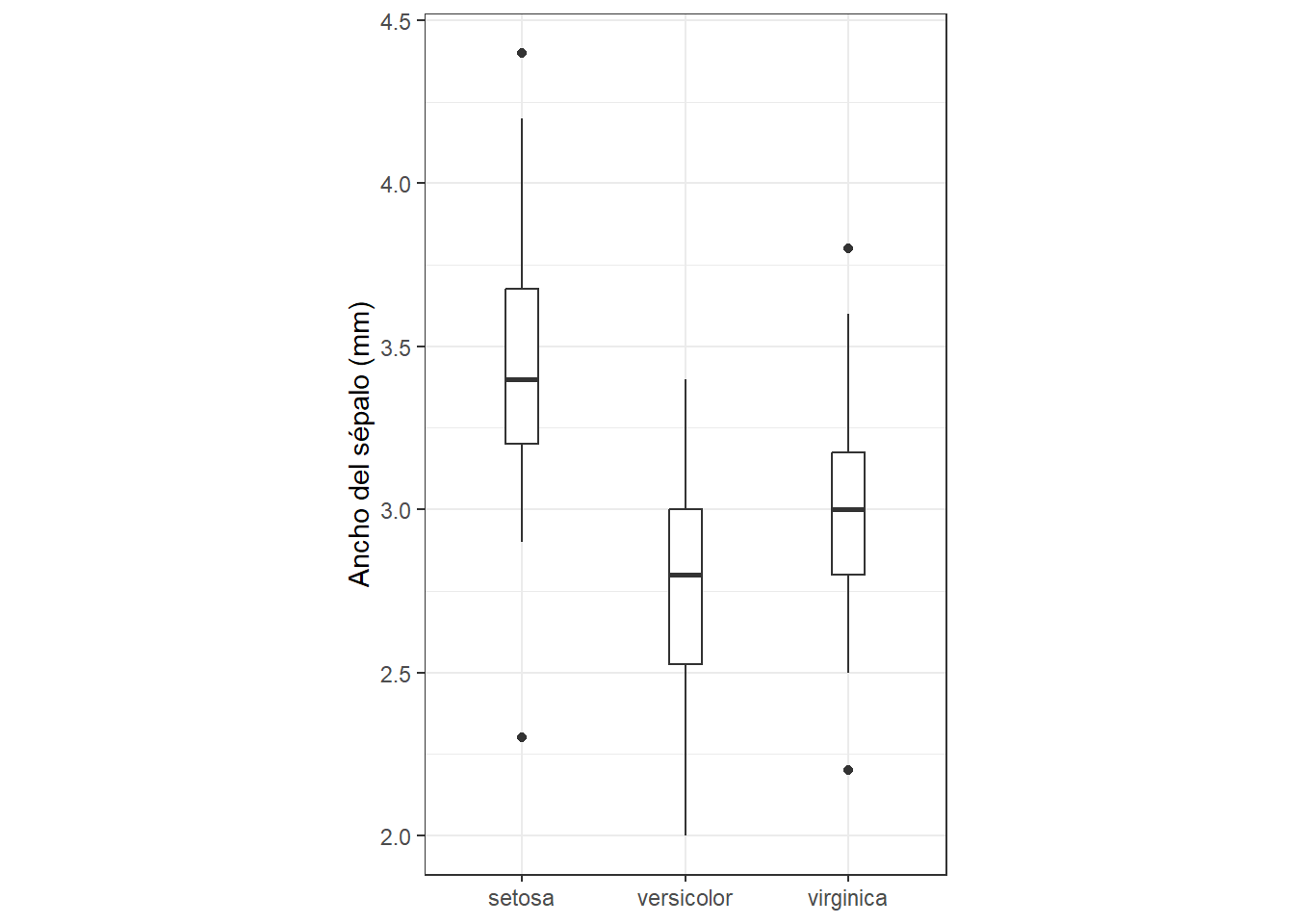
Vamos a empezar comprobando que al añadir coord_cartesian() nada cambia:

boxplot_base +
    coord_cartesian()

Mediante lo argumentos xlim e ylim podemos hacer zoom a una parte del gráfico. Esto difiere de la forma que vimos con las escalas en que aquí no se desechan los datos. Esto quiere decir que:

coord_*(xlim, ylim): se hace zoom a una zona del gráfico
scale_*_continuous(limits): se eliminan los datos fuera de los límites, y se recalcula el gráfico sin esos datos.

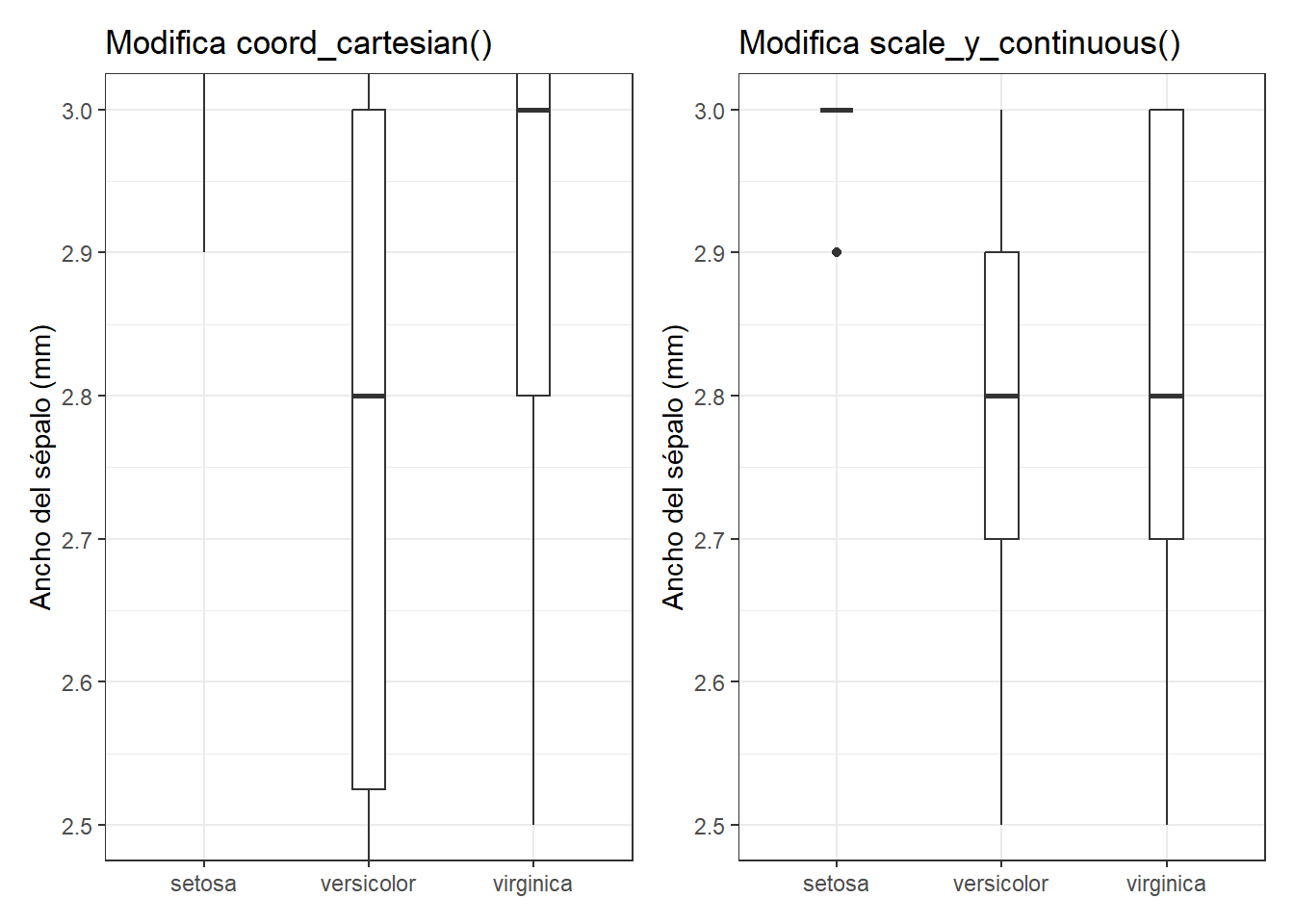
A continuación puedes ver un ejemplo donde en el primer caso se hace zoom real, mientras que en el segundo caso se recalculan los boxplot para ese área concreta.

g1 <- boxplot_base +
    coord_cartesian(
        ylim = c(2.5, 3)
    ) +
    ggtitle("Modifica coord_cartesian()")

g2 <- boxplot_base +
    scale_y_continuous(
       limits = c(2.5, 3) 
    ) +
    ggtitle("Modifica scale_y_continuous()")

g1 + g2

Por defecto, se añade un pequeño espacio antes y después de los valores más bajos y altos de x e y. Podemos eliminarlo con expand = FALSE, aunque en muchos casos esto no es nada útil:

boxplot_base +
    coord_cartesian(
        expand = F
    )

Aunque lo podemos hacer de forma manual en la mayoría de las ocasiones, tenemos una función que nos permite voltear los ejes:

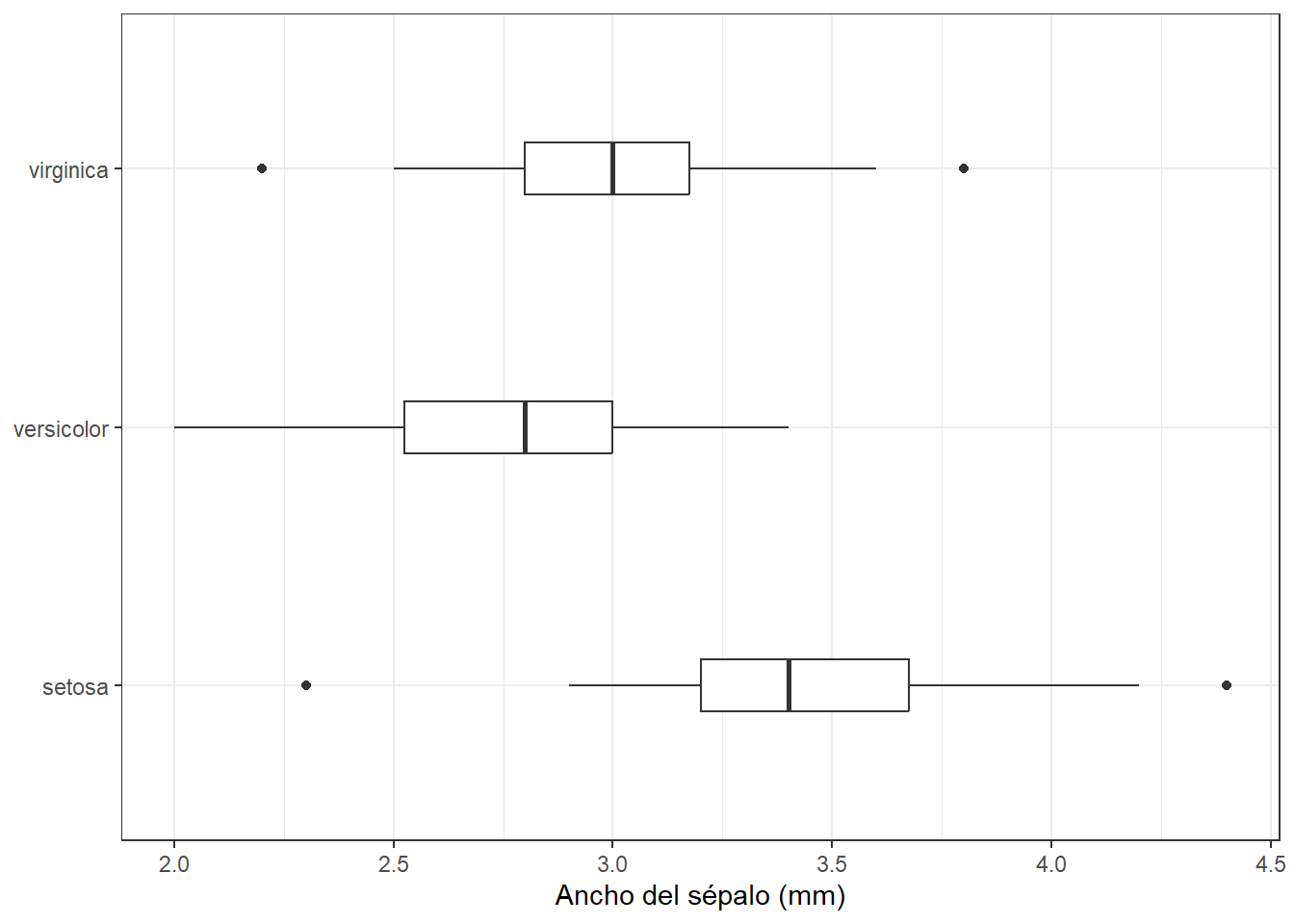
boxplot_base +
    coord_flip()

En este caso, una unidad del eje x es igual a una unidad del eje y. Esto es útil especialmente cuando las variables tienen la mismas unidades.

boxplot_base +
    coord_fixed()

También podemos modificar este ratio. En la siguiente figura, dos unidades del eje x son iguales a una unidad del eje y.

boxplot_base +
    coord_fixed(
        ratio = 2
    )

Y esto sería prácticamente todo lo que podemos hacer con los sistemas de coordenadas lineares.

8.2 Sistemas no lineares

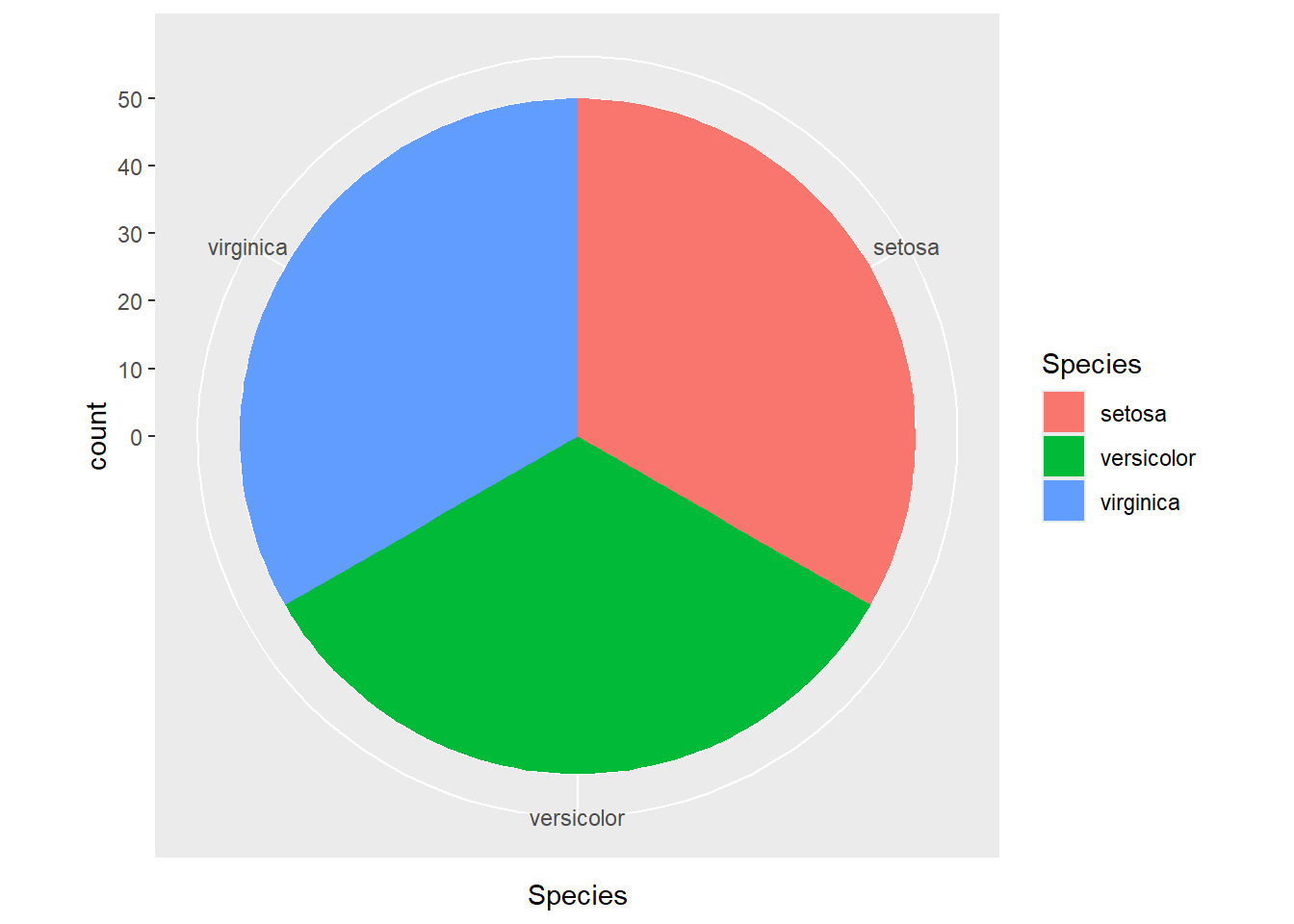
Estos sistemas puedes modificar la forma de las geometrías. Estos los utilizarás como menos frecuencia y en situaciones muy concretas. La función coord_polar() es la que nos permite crear los endemoniados gráficos circulares. Vamos a ver un ejemplo de lo que nunca debes hacer:

iris |> 
    ggplot(aes(x = Species, fill = Species)) +
    geom_bar(width = 1) +
    coord_polar()

Existen otras funciones que nos permiten crear sistemas no lineares. La más importante es coord_sf() que nos permite crear proyecciones de mapas. No obstante, esto queda fuera de los objetivos de este curso, así que no profundizaremos en ello.

8.3 Resumen

En este capítulo hemos visto cómo modificar los sistemas de coordenadas en ggplot2. Hemos visto cómo modificar los límites de los ejes, hacer zoom, voltear los ejes, fijar las escalas y modificar el ratio entre los ejes. Existen otras funciones que nos permiten crear sistemas no lineales, como coord_polar() para crear gráficos circulares y coord_sf() para proyecciones de mapas.

Wickham, Hadley, Danielle Navarro, y Thomas Lin Pedersen. 2021. ggplot2: Elegant Graphics for Data Analysis. Springer International Publishing. https://doi.org/10.1007/978-3-319-24277-4.